April 2024 | A longstanding problem in physics has finally been cracked by Professor Kostya Trachenko of Queen Mary University of London’s School of Physical and Chemical Sciences. His research, published in Physical Review E, unveils a general theory for predicting melting points, a fundamental property whose understanding has baffled scientists for over a century.
For decades, our physical understanding of the three basic states of matter – solids, liquids, and gases – relied on temperature-pressure phase diagrams. These diagrams depict the conditions under which each state exists, with distinct lines separating them. However, one crucial line, the melting line – marking the transition between solid and liquid – lacked a universal description.
Professor Trachenko‘s theory bridges this gap. By developing a new framework that incorporates recent advancements in liquid theory, he demonstrates that a simple parabolic equation can describe melting lines. This not only offers a practical tool for predicting melting points but also reveals a surprising universality across different material types.
This universality comes from observing that parameters in the parabolic equation are governed by fundamental physical constants such as the Planck constant and electron mass and charge.
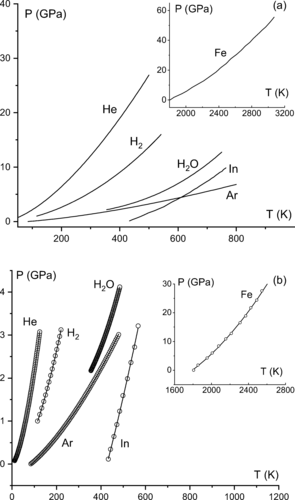
(a) Experimental melting lines (MLs) of Ar, He, H2 and H2O. (b) The same MLs in the low-pressure and low-temperature range (circles). / CC4 license, Source: DOI 10.1103/PhysRevE.109.034122
“The simplicity and universality of this result are particularly exciting,” explains Professor Trachenko. “It suggests that melting, despite its complexities, exhibits a fundamental unity across diverse systems, from noble gases to metals.”
This discovery holds significant implications beyond theoretical physics. Accurate prediction of melting points is crucial in materials science, with applications ranging from drug development to designing advanced materials and other areas where predicting phase diagrams is important. Professor Trachenko’s work paves the way for a deeper understanding of phase transitions and the creation of new materials with tailored properties.
More Information
K. Trachenko (2024), Theory of melting lines, Phys. Rev. E, vol. 109, iss. 3. doi.org/10.1103/PhysRevE.109.034122 (open access)
